この日は、見積もり伝票作成と工学的な勉強をしました。
<トルクについて>
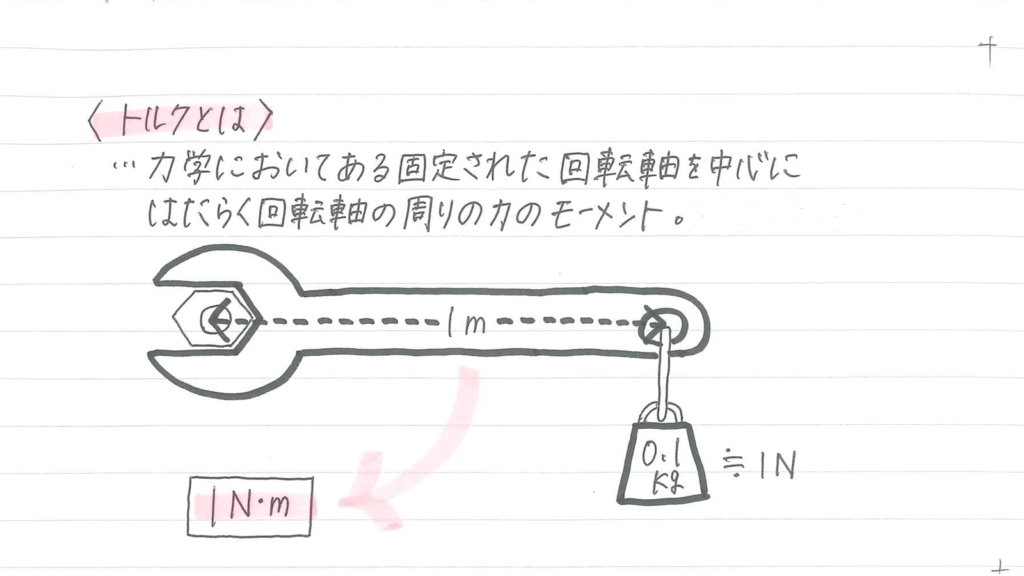
力学において、ある固定された回転軸を中心にはたらく、回転軸の周りの力のモーメント、ねじりの強さとも言われています。また力の単位はN(ニュートン)ですが、トルクの単位はN・m(ニュートンメーター)です。
身近な例では、ボルトやナットをしめるレンチを回す際に必要な回転力や、ペットボトルのキャップをしめるときの回転力などがそれにあたります。
トルクは【物体に加わる力】と【回転軸から力の加わる点までの距離】の積で求めます。【物体に加わる力】が同じとき、【回転軸から力の加わる点までの距離】が遠いほど、トルクが大きいことになります。
安田精機製作所の試験機では「プラスチック滑り摩耗試験機」や「ゲルタイムテスター」等は試験そのものにトルクが関わってきますし、「テーバー摩耗試験」や「テストミキシングローラー」等は機械内部の駆動にトルクが関わってきます。
トルクという言葉をよく耳にしますが、それが何かと聞かれると説明することができませんでした。トルクは自転車のペダルに例えると分かりやすく、競輪選手がペダルを漕ぐと、左右のペダルつなぐ車軸にものすごいねじり力がはたらきます。小さな子どもが漕ぐとたいしてねじり力ははたらきません。トルクを説明するうえで、この例えが一番分かりやすいのではないかと思いました!
こまちゃん、研修お疲れ様です!自転車の軸とは、面白い着眼点ですね!ただ、この表現はややトルクの本質を外してしまっていますよ。
トルクは「荷重の大きさ」に加え「軸からの距離」が影響するというのが面白いポイントです。
自転車のペダルを漕ぐ場合では、同じ自転車ならもちろん競輪選手のほうがより大きな荷重を与えることができるため、車軸に働くトルクは大きくなります。
しかしここで、子供用スペシャル自転車として、車軸からペダルまでの距離が長いものを用意すれば、漕ぐ力は弱くても「回転軸から力の加わる点までの距離」が大きいため、競輪選手と同じ、あるいはそれ以上のトルクを生み出すことができるのです。
そうなんですね!とてもよく分かりました。ところで、他にも日常生活でトルクの考え方を応用したものってありますか?
そうですね。まさに冒頭のレンチが代表的なものでしょうか。指でボルトを回しても、まったく締まりませんが、「回転軸から力の加わる点までの距離」をレンチで伸ばしてやることで、力を何10倍、何100倍にも増幅できるのです。
なるほど!原理だけでなく、具体的な例によってより深く理解することができました!これで私もトルクの説明ができそうな気がします!
